While the term “scientism” is often a rebuke to those considered to be overstepping the proper boundaries of science, plenty of scientists will plead guilty to the charge so long as they get a say in how the term is defined. The “scientism” that I defend is the claim that, as far as we can tell, all human knowledge is empirical, deriving from empirical contact with reality. Further, that empirical reality seems, as far as we can tell, to be a unified whole, and thus our knowledge of reality is also unified across different subject areas so that transitions between subjects are seamless.
What we call “science” is the set of methods that we have found, empirically, to be the best for gaining knowledge about the universe, and the same toolkit and the same basic ideas about evidence work in all subject areas. Thus there are no “other ways of knowing”, no demarcation lines across which science cannot tread, no “non-overlapping magisteria”.
A related but different stance is expounded by philosopher Massimo Pigliucci in his critique of scientism [1]. Pigliucci instead prefers the umbrella term “scientia”, which includes “science, philosophy, mathematics and logic”. This sees mathematics and logic as epistemologically distinct from science. Indeed Pigliucci has remarked:
it should be uncontroversial (although it actually isn’t) that the kind of attention to empirical evidence, theory construction, and the relation between the two that characterizes science is “distinctive enough” … to allow us to meaningfully speak of an activity that we call science as sufficiently distinct from … mathematics.
Mathematics is a huge area of knowledge where science has absolutely nothing to say, zip …” [2]
In this piece I argue that mathematics is a part of science. I should clarify that I am taking a broad interpretation of science. Nobody who defends scientism envisages science narrowly, as limited only to what is done in university science departments. Rather, science is conceived broadly as our best attempt to make sense of the empirical evidence we have about the world around us. The “scientific method” is not an axiomatic assumption of science, rather it is itself the product of science, of trying to figure out the world, and is now adopted because it has been found to work.
I will take one statement as standing proxy for the whole of mathematics (and indeed logic). That statement is:
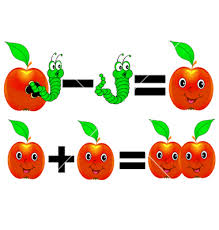
1 + 1 = 2.
Do you accept that statement as true? If so (and here I presume that you answered yes), then why?
I argue that we accept that statement as true because it works in the real world. All of our experience of the universe tells us that if you have one apple in a bag and add a second apple then you have two apples in the bag. Not three, not six and a half, not zero, but two. 1 + 1 = 2 is thus a very basic empirical fact about the world. [3]
It is a fact about the world in the same way that apples falling downwards are a fact about the world. There is no good reason to place these two different facts (gravity and maths) into two incommensurate domains of knowledge. Our understanding of both derives from empirical reality, and thus both are equally “scientific”.
Having asserted that, let me argue against possible alternative answers to my question of why we accept that 1 + 1 = 2.
Maths is derived from axioms
One answer — perhaps the commonest — asserts that maths is not derived from empirical observation but instead derives from axioms. You might assert that you accept 1 + 1 = 2 because it is proven so from the basic axioms of maths. You might point to Peano’s axioms and assert that from those one can logically arrive at 1 + 1 = 2. [4]
My first reply is that I don’t believe you. I don’t believe that there was a time in your life when you were dubious about the assertion 1 + 1 = 2, but then consulted Peano’s axioms, and after some logical thought concluded that, yes, 1 plus 1 really must equal 2. I assert that you accepted 1 + 1 = 2 long before you knew anything about Peano’s axioms, and that you accepted it because it works in the real world: if you had two sweets you could give one to your pal and eat the other yourself. [5]
But, even if your belief that 1 + 1 = 2 does derive from axioms, whence your faith in those particular axioms? How and why did Signor Peano arrive at that set of axioms? I assert that they were arrived at with the fact of 1 + 1 equalling 2 being a necessary consequence. Had Peano’s axioms resulted in 1 + 1 equalling anything other than 2 then the axioms would have been rejected as faulty. Signor Peano would have been told to go away and come up with axioms that worked (ones compatible with the non-negotiable truth that 1 + 1 really does equal 2).
Thus, the axioms mathematicians adopt are not arbitrary, chosen by whim or fiat, they are chosen to model the empirical world. Mathematics is thus distilled empiricism. The same can be said about logic and reason. In order to get from Peano’s axioms to derived results you need to use logical reasoning. What validates that logic and that reasoning? Again, I assert that empirical reality validates them. The reason that we adopt logical axioms such as the law of non-contradiction is that they hold in the empirical world. [6] How else would we know which logical axioms to adopt? Thus the whole edifice of mathematics and logic is a distillation of empiricism, created and developed as a model of the basics of how our world works.
Mathematics is arbitrary
Nevertheless, some might assert that no, mathematics is a self-contained logical system entirely distinct from empirical reality, and that any correspondence between mathematics and science is simply a coincidence. Some might even assert this with a straight face. It leads to puzzlement over what Eugene Wigner called “the unreasonable effectiveness of mathematics” when applied to science, but there is no puzzle if mathematics describes deep properties of our empirical universe and is derived from that universe. The idea that mathematics is arbitrary and independent of our universe would be more convincing if mathematicians spent as much time pursuing maths based on 1 + 1 equalling six and a half as they do with 1 + 1 = 2.
A more sophisticated version of this answer accepts that mathematics originally derived from our universe (with, for example, Pythagoras’s theorem resulting from drawing on bits of paper, or from attempts to get a building’s walls square), but points out that nowadays mathematicians experiment with all sorts of axioms that are not first suggested by observation.
As an example, consider the generalisation of the “flat” geometry developed by Euclid to the “curved” geometries developed by Carl Gauss, Bernhard Riemann and others. The relaxing of the parallel-line postulate of Euclid to produce non-Euclidean geometries was not motivated by observations but by thinking about the structure of the axiomatic system. Surely this is a non-empirical approach that distinguishes mathematics from science?
Well no. Theoretical physicists do this sort of thing just as much as mathematicians. They take their set of empirically derived axioms (though in physics these tend to be called “laws” rather than “axioms”) and think about them; they experiment with different axioms/laws and work out the consequences. Often they are not immediately motivated by a match to observations but are following their intuition.
They are still, though, working with an axiomatic system that is essentially distilled from the empirical universe, and they are using an intuition that is also very much a product of the empirical universe. Curved geometry — developed by the mathematician Riemann — was later found to be useful in describing the universe when the physicist Einstein — also following a path of logic and intuition — developed the theory of General Relativity. If anyone wants to draw a demarcation line between domains of knowledge, the line would not be between the mathematician Riemann and the physicist Einstein.
Why is it that mathematicians’ intuitions so often produce mathematics that is later found to be useful to physicists? I argue that their experimentations with axioms are productive because their logic and intuitions are also empirical products. Thus a mathematician has a good idea of which changes to axioms are sensible and which are not. Allowing parallel lines to diverge (and thus producing non-Euclidean geometry) is sensible; adopting “one plus one equals six and a half” is not. [7] In both mathematics and physics, if the experimentation produces results that are nonsensical when compared to our universe then they will not be pursued. The empirical universe is in both cases the ultimate arbiter.
At the cutting edge it can, of course, be unclear whether maths and/or physical theories “work”. A current example is string theory, where a generation of theorists is exploring the mathematics of strings. Maybe it’ll lead to new physical theories unifying quantum mechanics and gravity, and maybe not. At the moment, though, one could not really say whether string theory was “mathematics” or “theoretical physics”. This emphasises the seamless transition between those fields, with string theory straddling the (arbitrary and unmarked) boundary.
An aside before proceeding. Gödel’s incompleteness theorem tells us that even if we have a set of axioms such as Peano’s axioms, which underpin the natural counting numbers and which yield the statement that 1 + 1 = 2, there will be other statements about the natural numbers which are true, but which cannot be shown to be true from the axioms. A further result tells us that the axioms cannot be used to show that the system built from those axioms is consistent. This fundamental limitation of an axiom-based approach shattered hopes of mathematics ever being a complete, consistent, self-validating and self-contained system.
From a scientific point of view, with mathematics being seen as a part of science, such limitations are unsurprising. Science is derived from empirical evidence and our available evidence will always be a small and incomplete sample of the universe, and thus scientific results are always provisional, in principle open to revision given better data.
But mathematicians spend their time exploring axioms that may be unrelated to the empirical world
This is true. But then so do many theoretical physicists (ask any string theorist)! Such a mathematician may not care about correspondence with reality, but is simply exploring the results of different axioms for fun.
If we ask what the human brain evolved for, it evolved to assimilate sensory data, to model those data, to perform deductive reasoning on those data, and to run “what if?” simulations as an aide to decision making. E.g. “If I do X how will others react?”. Such “what if?” simulations are based on empirical reality, but then simulate possible variations on that reality. For example, all humans like stories, and a novel can be considered a “what if?” alternative reality, in which the characters and events are not “real”, but are the sort of things that could be real.
Mathematics is like this. It is ultimately based on truths that we arrived at empirically. But then mathematicians explore the consequences of those truths, and perform “what if?” simulations in which they consider alternative realities. For example they may think about 5-dimensional space rather than the usual 3-dimensional space. This mathematics is “about” the empirical world in the same way that Jane Austen’s Pride and Prejudice is “about” the real world.
That is not to say that a 5-dimensional orthoplex is a “real” object any more than Mr. Darcy is a real person, but the whole enterprise is still very grounded in the empirical world. If an axiom or an avenue of mathematics becomes nonsensical in comparison to the empirical world then it is simply not pursued and is regarded as uninteresting. The fact that many “abstract” areas of mathematics have later been found to have useful physical applications just shows how good mathemiticans and their empirically grounded intuitions are at judging “what if?” scenarios.
Our maths is the product of pure logic, deriving only from human intuition
Many will disagree with me and assert that human intuition is a primary source of knowledge, distinct and separate from empirical evidence. Indeed this idea is popular with some philosophers, who argue that introspection and thought are the wellsprings of their philosophical knowledge, and thus that philosophy is a domain distinct from the empirical domain of science. [8]
However, what basis do we have for supposing that our human intuition produces accurate knowledge about the universe? The first reason is that our intuition has been developed and honed over our lives based on our sense data about the world around us. Thus our intuition is very much an empirical product.
Further, we can ask about instinct (that portion of our intuition that is not the product of life experiences, but is encoded in the genes). Our genetic programming will also be a product of empirical reality. Our brains are the product of evolutionary natural selection, and thus have developed to make real-time decisions that aid survival and reproduction. Obviously decision-making that bore no relation to the real world would be useless, and thus we can have some confidence that our intuitions are to a large extent programmed to produce decisions well-aligned to empirical reality.
Of course natural selection is not a perfect programmer, and anyhow is not aiming at a perfect and unbiased decision-maker, it is aiming at the one best at survival and reproduction. Thus we would expect our intuition to be reliable only with respect to the everyday world relevant to survival and reproduction, and to be unreliable about aspects of the universe (such as quantum mechanics and general relativity), that are irrelevant for everyday life.
We’d thus expect our intuition to be a folk metaphysic, good enough for many purposes, but full of biases and foibles, particularly so where an inaccurate assessment might actually aid survival and reproduction. An over-active pattern-recognition detector and the Lake Wobegone effect are likely examples of this. Visual illusions such as the checker-shadow illusion show how easily the human intuition is fooled, in this case precisely because the human intuition is making some assumptions about how the world works, and thus about lighting and shading. [9]
A critic might, though, accept that some of our intuitions are related to empirical reality, but then argue that intuition also gives access to knowledge that is not empirical and cannot be arrived at by empirical means. My response is to ask what basis the critic has for that assertion and what reason he has for supposing that “non-empirical knowledge” has any reliability or validity.
From the evolutionary perspective we have no good reason to suppose that intuition is anything other than an imperfectly and empirically programmed device that models the empirical world — after all, failing to find enough to eat, ending up eaten by a predator, or finding a mate and successfully rearing children, are all aspects of a brute empirical world. Thus we should accept intuition as a useful “quick guide to reality”, but ultimately we should not accept human intuition except where corroborated by empirical evidence. Indeed, the whole point of the scientific method is to use empirical evidence to do much better than just consulting our “quick guide” intuition. [10]
Our maths is the only possibility
The last alternative answer that a critic might advance [11] is that we accept the claim that 1 + 1 = 2 because it must be true, it is the only logical possibility. Thus, such a critic will say, 1 + 1 equalling six and a half is simply nonsensical. Such a person would not merely be asserting that it is impossible in our world, but that it is impossible in all possible alternative worlds.
Do we know this? And, if so, how? Has anyone given a logical proof of the impossibility of such an alternative scheme? Any such proof could not use any axiom or logic derived from or validated by our empirical world (that would only show that such alternatives did not occur within our world). But without that, how would one go about showing that the logic of our world is the only one possible?
One could not use our-world logic for such a task and nor could we use human intuition, since our intuition is very much derived from and steeped in the logic of our own empirical world — indeed our brains have evolved precisely to model the logic of our world — and thus we would not expect them to be in any way useful for contemplating radically different alternatives.
But, even if we were to grant the claim that our world’s logic is the only possible system of logic, that would still leave the question of how we came to learn about that logic. And the only plausible answer is that we learned from observation of the empirical universe and thence deduction about the logic by which it operates.
Further, even if mathematics is “necessarily true” that does not necessarily distinguish it from empirical science. For all we know, laws of physics might be “necessarily true” in the same way. At a deep level a theoretical-physics description of fundamental particles and the properties of space and time is a mathematical description. [12] While some philosophers distinguish “necessary” mathematical truths from “empirical” facts about science, this distinction seems less and less appropriate as physics develops. Pigliucci states that:
There are mathematical explanations for why certain things are impossible (like crossing all the bridges of the town of Königsberg exactly once) which trump, or make superfluous, or are more basic than, any scientific (i.e., empirical) explanation.”
Pigliucci references an article by Marc Lange [13] which distinguishes “distinctively mathematical” explanations from “causal” scientific explanations. Yet such “distinctively mathematical” explanations are commonly used in science, a typical explanation being: “because the laws of physics are invariant under the Lorentz transformation” (where the Lorzenz transformation is mathematical).
Or take the question: “why does there not exist a particle consisting of three up-quarks with a spin of 1/2 and a mass similar to that of the proton?”. The answer is that there is no way of making such a combination have a wavefunction that is anti-symmetric under exchange of any two particles. This is a “distinctively mathematical” explanation of exactly the bridges-of-Königsberg type, but is also the sort of explanation that fundamental theoretical physics increasingly arrives at. The explanation is not in terms of causes but in terms of deep axioms/principles/laws, such as the need for a wavefunction to have a definite symmetry.
But, if we ask further why such a particle can’t have a mixed symmetry we can only resort to the empirical fact that they don’t occur in nature. Similarly, a “distinctively mathematical” explanation for why one cannot cross the bridges of Königsberg exactly once relies on axioms for which the only ultimate validation is empirical.
Conclusion
I have argued that all human knowledge is empirical and that there are no “other ways of knowing”. Further, our knowledge is a unified and seamless sphere, reflecting (as best we can discern) the unified and seamless nature of reality. I am not, however, asserting that there are no differences at all between different subject areas. Different subjects have their own styles, in a pragmatic response to what is appropriate and practicable in different areas. For example, a lab-based experimental science like chemistry has a very different style to an observational science like astronomy. [14] Further, biochemists studying detailed molecular pathways in a cell will have a very different style to primatologists studying social interactions in a wild chimpanzee troop.
Such differences in style, however, do not mandate that one of those subjects be included within “science” and another excluded. The transitions in style will be gradual and seamless as one moves from one subject area to another, and fundamentally the same basic rules of evidence apply throughout. From that perspective mathematics is a branch of science, in the same way that so is theoretical physics. Indeed, some theoretical physics is closely akin to pure maths, and certainly far closer to it in style and content than to, say, biochemistry. The different subject labels can be useful, but there are no dividing lines marking the borders. No biochemist worries about whether she is doing biology or chemistry, and string theorists don’t worry much whether they are doing maths or physics.
Thus, in arguing that a subject lies within the broad-encompass of “science”, one is not asserting that it is identical in style to some branch of the generally-accepted natural sciences, but that it belongs to a broad grouping that spans from studying molecules in a chemistry laboratory, to studying the social hierarchies of a baboon troop, to theoretical modelling of the origin of the universe, and that it belongs in that group because epistemologically the knowledge has the same empirical source.
I thus see no good reason for the claim that mathematics is a fundamentally different domain to science, with a clear epistemological demarcation between them. This same set of arguments applies to the fields of reason and logic, and indeed anything based on human intuition. All of these seem to me to belong with science, and all derive from the same source, our empirical experience of the universe and our attempts to make sense of it.
————————-
[1] Massimo Pigliucci, Midwest Studies in Philosophy 37 (1):142-153 (2013) “New Atheism and the Scientistic Turn in the Atheism Movement”.
[2] See Pigliucci’s article Staking positions amongst the varieties of scientism.
[3] A pedant might point out that in modular arithmetic, modulo 2, 1 plus 1 would equal 0. I am taking 1 + 1 = 2 to refer to simple counting numbers; one apple plus one apple equals two apples. If we ask further about the basic concepts of “1”, “2”, “+” and “=” I would again base them on patterns discerned in the empricial world, which is of course how humans first came up with those concepts.
[4] Giuseppe Peano, 1889. Arithmetices principia, nova methodo exposita. Wikipedia account
[5] A pedant might point out that that equates to 2 – 1 = 1, not to 1 + 1 = 2.
[6] Indeed the great Islamic polymath Avicenna wrote, c AD 1000, that: “Anyone who denies the law of non-contradiction should be beaten and burned until he admits that to be beaten is not the same as not to be beaten, and to be burned is not the same as not to be burned”, a direct derivation of logic from empirical experience!
[7] The Axiom of Choice is an example of an axiom adopted largely because it feels intuitively right to mathematicians, plus they like the results that it leads to.
[8] There is a vast philosophical literature on this issue, with Kant’s Critique of Pure Reason being influential.
[9] For the Lake Wobegone effect see the this wikipedia article. For the checker shadow illusion see here.
[10] An obvious example being the need for double-blinding in medical trials, which originated from the realisation of how unreliable human intuition, based on anecdotes and a partial memory, actually is.
[11] Unless you have other alternative answers?
[12] See Tegmark, Max, 2014 “Our mathematical Universe” for pushing this argument all the way.
[13] Marc Lange, 2012, What Makes a Scientific Explanation Distinctively Mathematical?
[14] One should ignore commentators who over-interpret overly-simplistic accounts of the “scientific method” and claim that only lab-based experimental science counts as science.



I accept it as true, because that is the definition of “2”. So it is true by definition.
No, it isn’t.
Counting is a very useful method in the real world. But arithmetic is not counting. Rather, arithmetic idealizes counting. Actual counting in the real world gives you such things as hanging chads.
That cannot be right, because the axioms are themselves part of mathematics. So unless axioms come from axioms, mathematics cannot be said to come from axioms.
One could perhaps say that mathematics comes from idealizing empirical methods. But that, also, cannot be correct. For, in practice, some empirical methods come from the mathematics rather than the other way around.
I don’t have a problem with including mathematics as part of science. There is at least a case for that. But mathematics is not empirical, and that’s important.
Here’s roughly how I look at it. Science is systematic, and that’s an important point about science. Mathematics is the theory of systematicity.
I sometimes like to put it this way: The correct spelling of “epistemology” is M A T H E M A T I C S. The philosophers don’t seem to understand this.
Science is more than systematic. It also has to do with ‘seeing’ where particular systems apply and where they do not and devising alternative systems and in this sense is very close to mathematics which strives to formally describe and explore in abstract terms relations among defined parameters. Science, especially biological science, has difficulty even defining parameters most of the time and thus requires a very flexible mind. The word Systematic allows only part of that process.
I appreciate this exposition. I’m not really sure how somebody in the “other ways of knowing” crowd could respond to this, but hopefully somebody will offer a good rebuttal. Certainly a tall order for the other side.
I broadly agree with Neil. Arithmetic is historically rooted in experience, but has been idealized to the point where it stands independent of the real world.
It seems likely that people started counting things because they found that practice useful. At some point they must have noticed that they could combine counts. For example, I can count my 3 goats in one field and my 2 goats in another field, or I can count all my goats in one go, and get 5. So (in this instance) 3 goats and 2 more goats makes 5 goats. And before long they must have realised that such relationships were consistent, not just across different instances of counting goats, but across instances of counting anything countable. Thus was born basic arithmetic. Once you abstract away from counting particular things (like goats and apples), arithmetic no longer has any essential link to physical reality. I can apply “2+3=5” to goats, but I can also just state it as a fact in its own right, not applied to anything. I can also apply it to purely abstract countable concepts, such as the roots of equations. This is “pure” mathematics.
Coel writes: “Thus, such a critic will say, 1 + 1 equalling six and a half is simply nonsensical. Such a person would not merely be asserting that it is impossible in our world, but that it is impossible in all possible alternative worlds…. Do we know this? And, if so, how?”
It’s our practices with words that give them their meaning. In the case of number words, it is primarily our practice of counting which gives them their meaning. We count: “1,2,3,4…” and by virtue of this, the number which comes after 1 is 2. By virtue of our practices with counting and adding, n+m is what you get if you count n items and then count another m items. So 1+1 necessarily gives you the number after 1, which is 2. The only way to make “1+1=3” true is to change the meaning of at least one of those terms. But that wouldn’t change the facts; we would just be expressing the same facts in a different language (or talking about different facts). If we imagine a world where people counted, “1,3,2,4…”, then for those people it would be correct to say “1+1=3”, but their “1+1=3” would mean the same as our “1+1=2”. The underlying fact would still be the same.
P.S. I meant that I agree with Neil Rickert. Surname-less Neil seems to be another person.
Hi Richard,
Yes, you can interpret “1 + 1 = 3” is simply using the word “3” to mean “2”, but that wasn’t what I was meaning. I was envisaging a world where if you add 1 unit to 1 unit you really do get 3 units (with “3” meaning what we mean by three). Is that possible? Well it is not possible in our world, of course, but can we really rule out an alternative logic system working like that?
Anyhow, the idea is not totally alien to us. For example, the power of sound waves goes as amplitude squared. Thus if you add a sound wave with a power of 1 unit, in phase with another sound wave of power 1 unit, the result is a sound wave with a power of 4 units.
Hi Coel,
“Well it is not possible in our world, of course, but can we really rule out an alternative logic system working like that?”
Yes, we can. I attempted to explain why. 1 + 1 = 2 is a necessary consequence of the meanings of those symbols. In any system where the sentence “1 + 1 = 3” is true, at least one of those symbols must have a different meaning from the meaning it has to us.
“Thus if you add a sound wave with a power of 1 unit, in phase with another sound wave of power 1 unit, the result is a sound wave with a power of 4 units.”
What’s the relevance of this? We could invent a mathematical language which idealized such facts, in which “1 + 1 = 4” would be a true sentence. That would be a different language from the one in which we correctly say that 1 + 1 = 2. The symbol “+” would have a different meaning in the new language, and to avoid confusion it would be better to use a different symbol, writing for example “1 @ 1 = 4”. This is irrelevant to the fact that 1 + 1 = 2.
It may be helpful to look at systems where we already use the same word in more than one sense. Consider the various systems of geometry: Euclidean and several non-Euclidean geometries. A sentence which is true in one of those systems may be untrue in another system. That’s because the symbols in the sentence have different meanings. “Line” in Euclidean geometry does not mean quite the same thing as “line” in a non-Euclidean geometry. The different systems of geometry speak different languages.
Hi Richard,
I guess it is true that the symbols would have to be slightly different, but they could still map pretty much to what we mean by them.
Consider a hypothetical world in which: You take one apple and place it in an empty bowl. You then take another apple and place it in the bowl besides the first apple. There are now three apples in the bowl (and by “three” there I do mean what we mean by “three”, rather than simply using the word “three” to mean “two”).
In that scenario, all of the terms map pretty much to our understanding of them. What is radically different is the way that world works.
Hi Coel,
I’m having difficulty making sense of that. The first part of your sentence sounds like it’s agreeing with something I said, but I wasn’t talking about different symbols. If I ignore the confusing first part of your sentence, it sounds like you’re simply denying my assertion (without giving any reason for doing so). But the strangeness (to me) of your reply suggests that you misunderstood me.
But you didn’t use all the relevant terms. You didn’t use the terms “+” and “=”. You discussed a physical scenario, and not any arithmetic facts.
I would strongly recommend that you re-read my first comment, because I explained my position fairly carefully there, and I don’t think you took it on board. If there’s anything there you disagree with or don’t understand, let’s discuss those points specifically.
P.S. How do you mark up quoted passages here. I used “quote” in angle brackets, but that didn’t work. (And, sorry, I replied in the wrong place, so my reply didn’t get appended to our conversation.)
Hi Richard,
Let’s consider the two worlds: our world, and the alternative world described in my last comment (adding one apple plus one apple to an empty bowl gives three apples).
In that case, you are entirely right to assert that our-world-maths is entirely unaffected by that. Our-world-maths, treated as a self-contained logical system, would still have 1 + 1 = 2, because that follows from the axioms/definitions of our-world-maths.
Is the last paragraph what you are asserting, because if so then we are in complete agreement?
But, I am then asserting that mathematicians in that alternative world would not have developed our-world-maths, they would have developed alt-world-maths, in which 1 + 1 = 3. The symbols in alt-world-maths would have some sort of rough equivalence to our-world-maths, but they would still be separate and distinct systems with different axioms.
The assertion I am making from this is that the axioms of our-world-maths are chosen to match empirical reality and that other logical systems are possible (e.g. those of alt-world), but that our-world mathematicians choose not to pursue them because the whole enterprise of mathematics is steeped in the empirical reality of our world.
( For quoting I use html “blockquote” in angle brackets; I’ve added them to your last comment.)
Hi Coel,
I’m a bit disappointed you didn’t respond regarding my first comment. I’ll press on and respond to your latest reply, hoping that my response will help clarify and elaborate on my original comment. But I think this will be my last.
I’m saying that the truth of “1 + 1 = 2” is a necessary consequence of the meanings of those terms. They get their meanings mainly from our practices with them, not from axioms or definitions. In adopting those practices we have adopted a certain logical system, the one we call arithmetic. So you could also say that the truth of that statement is a necessary consequence of the logical system we’ve adopted. And you could say that the logical system fixes the meanings of the terms.
They might adopt some logical system modelled after the strange physical behaviour that you’ve described. But there’s no reason they can’t also adopt arithmetic as we know it. Whether or not they also develop our arithmetic, the logical system you’re hinting at is a different one from ours, and “1+1=3” in their logical system does not mean the same thing as “1+1=3” in our logical system. If we assume that their number words and their “=” mean the same as ours, we can consider their “+” to be just another arithmetic operator, alongside our “+”, “-“, “x”, etc. To avoid confusion we should give it a different symbol, say “$”, and write “1 $ 1 = 3”. Try working out in full the rules of that logical system. That might help you to see that you’ve just created a new operator, to which you’ve misleadingly given the same name as pre-existing operator. The aliens’ “+” is not our “+”, and you’re conflating two different meanings of “+”.
You don’t have to invoke another universe to find different logical systems that recycle the same symbols (and sometimes cause confusion in doing so). I mentioned different geometries that share the word “line”. A “line” in one geometry is not quite the same thing as a “line” in another geometry. The different concepts of “line” have enough in common that we are inclined to use the same word. But if we make the mistake of thinking they are the same concept, we will make the mistake of thinking that statements of one geometry sometimes contradict statements of another. When we talk within the context of different geometries, we are speaking a subtly but significantly different language.
Hi Richard,
Yes, ok, I agree.
Just as there is no reason why *we* can’t adopt *their* logical system modelled after their strange physical behaviour. Indeed, this is the central point I am making, that we have adopted a logical system modelled after our physical reality.
Ok, I can happily accept calling the alt-world operator “$” and thus writing 1 $ 1 = 3. Thus, in our world the “+” symbol maps to the operation of adding one apple to a bowl followed by another apple. And in alt-world the “$” symbol maps to the operation of adding one apple to a bowl followed by another apple.
So, let me now define “&” as mapping to “the operation of adding one apple to a bowl followed by another apple” in whatever world we’re dealing with. In our world we then have 1 & 1 = 2 and in the alt-world we have 1 & 1 = 3.
That is essentially what I’ve meant all along by “+”, namely a logical symbol that maps to the physical reality of the universe under consideration, but if you prefer to use different symbols to denote the different physical behaviours in the two universes then ok, fine. That doesn’t alter my essential point that our logical system is adopted precisely because it models our physical reality.
Hi Coel,
I’ll continue a little longer, as I feel we might be making some progress.
If you re-read my first comment, you’ll see that the question I set out to address was whether 1+1 could equal something other than 2 in a different universe. If you’re discussing some other question, then we’re talking at cross-purposes. If you agree with me that 1+1 could not equal anything other than 2, then my job is done.
With regard to the question I’m addressing, it makes no difference why we adopted a particular logical system. Once we’ve adopted that system, the meanings of its terms are fixed. So the meaning of our “1+1” is fixed. If someone else (in this universe or another) adopts a different logical system, which happens also to use those symbols, their meanings of the symbols will be different, so their “1+1” does not mean the same as our “1+1”. They are speaking a different language from us.
Similarly, there could (in principle) be a country where people speak Schmenglish, a language just the same as English, except that the meanings of the words “round” and “flat” are reversed. In Schmenglish it would be true to say “The Moon is flat”. But, if you said there could be a country in which the Moon is flat, you would be talking nonsense. The shape of the Moon is not the sort of thing that can be relative to a country, so it’s a misuse of language to speak as though it is. Similarly, it’s a misuse of language to say there could be a universe in which 1+1 equals 3, notwithstanding the fact that in some other universe people could speak a different language in which it would be true to say “1+1=3”. (Anyway, people could speak such a language in our own universe, so introducing an alternative universe is a red herring.)
Does this mean you accept that “$” does not mean the same as “+” as we normally use that term? So the fact that 1$1 equals 3 does not license our saying that 1+1 could equal 3 in another universe, even if the aliens in that universe happen to use the symbol “+” to mean $?
Would you similarly accept that your new concept “&” does not mean the same as “+” as we normally use that term? (I find your definition of “&” extremely unclear, but I can find no interpretation that makes it equivalent to “+” as we normally use that term.) So even if 1&1 equals 3 in the other universe, this does not license our saying that 1+1 equals 3 in that universe? You claim that you’ve been using “+” to mean “&” all along, but if I treat that claim as true (for the sake of argument), you’ve been speaking an idiosyncratic language and misleading all your readers, who naturally assumed that when you said “+” you meant +, as we normally understand it. If you continue speaking that language, then “1+1 equals 3 in that universe” might be a true statement in your language. But you still haven’t established that 1+1 can equal 3, in the normal sense of those words.
Hi Richard,
Yes, we have been talking at cross-purposes. If you’re saying that “if we adopt our logic system then 1 + 1 cannot be anything other than 2” then I agree entirely. If we then say: “If, in some other universe, we still adopt our logic system, then we still get 1 + 1 = 2”, then again I agree, though the words “in some other universe” don’t actually do anything in that sentence.
By “in a different universe” I meant “in the different logic system that would map to that different universe”. Thus by “1 + 1 = 3” I was referring to the *alternative* logic system, which uses different definitions and axioms, that mathematicians would have developed in their alternative reality. I wasn’t suggesting that if you transport our logic system somewhere else then it starts operating differently.
The reason that I was using the same symbols for both was the suggestion that both would result from a simple task such as “adding one apple to a bowl followed by another apple”, and that the different axioms and definitions would have been chosen to map to the different physical outcomes.
If you mean “1 + 1” to refer to *our* logical system then of course it could not be anything other than 2, and of course we would not be licensed to say that “1 + 1 = 3”.
But I am not using “1 + 1 =” to refer to *our* logical system, I am also considering other possible logical systems. If you like consider the following definitions:
Start with an empty bowl:
“1” maps to “add an apple to the bowl”
“+” maps to “now continue”
“1” maps, as above, to “add an apple to the bowl”
“=” then maps to “count the apples”.
Would you accept that with those definitions then the outcome can be 2 in our-world and 3 in alt-world?
Hi Richard,
To explain why I’m finding this conversation somewhat baffling, here is an analogous conversation:
Me: Let’s consider a counter-factual alternative history in which Romney beat Obama in the last election and became US President.
You: But the only way that could have happened is if history had been different.
Me: That’s what I’m considering.
You: But if, in this alternative history, all the actual historical events were the same, then Obama would still win.
Me: But I’m considering an alternative history in which the historical events were not the same, and indeed were different.
You: But the meaning of the names “Obama” and “Romney” is to refer to people in *our* history. If we’re not talking about *our* history then they are not “Obama” and “Romney”.
Me: OK, let’s call them alt-Obama and alt-Romney in this alternative history, if it makes things clearer.
You: But it’s still the case that in *our* history with *our* Obama and Romney, there is no possible outcome other than an Obama win.
Me: Yes, entirely true, and entirely misses the point of what I’m trying to consider.
Is the above unfair to you?
Hi Coel,
Thanks for your reply. Sorry, I didn’t find your alternate history conversation helpful. Talking at cross purposes is very common in philosophy, because it’s so difficult to avoid ambiguity on these tricky matters, and so misunderstandings are rife. I’ve spent many hours (too many) choosing my words carefully, and I’m sure I’ve still been unclear at times. If you’ll pardon me for saying so, you’ve clearly spent much less time on your comments than I have (understandably) and I find them often highly ambiguous.
My only problem here is with your addition of the conditional clause “if we adopt our logic system”. I think that’s superfluous and potentially misleading. We should simply say that 1 + 1 cannot be anything other than 2. Can you agree to that?
We say the Moon is round, without having to add “if we adopt English and not Schmenglish as our language”. It’s taken for granted that we are speaking English and using words in their standard senses, unless we indicate otherwise. As long as we’re using words in their standard senses, we can only correctly say “1 + 1 = 2” and not “1 + 1 =3”. So it’s sufficient to say that 1 + 1 cannot be anything other than 2.
I have more serious problems with some things you say later in your comment. But if you’re willing to say without qualification that 1 + 1 cannot be anything other than 2, then I’ll be content. In any case, this really will be my last comment on the subject. These sorts of discussions take up far too much time. I really should give them up, and spend my time on something more useful. 😉
Hi Richard,
I entirely agree that if we’re speaking “our-maths” then 1 + 1 = 2, necessarily so. By suggesting “1 + 1 = 3” I was indeed considering speaking a different language, an alternative-world maths, based on different axioms, mapping to an alternative-world physics. Maybe I should tweak the article to make it more obvious that that’s what I meant.
Cheers, Coel.
Hi Coel,
I can’t resist commenting again, because you’ve “agreed” with something that is not my position.
I’m afraid that isn’t agreeing with me. That’s the very kind of statement that I just objected to, i.e. one that’s made conditional on what language we’re speaking. What I’m saying is just this: 1 + 1 = 2, necessarily so.
I can’t resist having one more try at explaining…
As I see it, you’re conflating two different ideas:
A1. There are possible languages in which it’s correct to say the sentence (the sequence of symbols) “1 + 1 = 3”.
A2. 1 + 1 can equal 3.
A1 is trivially true, since we can invent a special-purpose language to make any sequence of symbols into a true sentence. A2 is false (or perhaps incoherent), because it’s expressed in English, and given that we’re speaking English, we cannot correctly say that. When we’re speaking English we can only correctly say “1 + 1 equals 2”. If we cannot correctly say “1 + 1 equals 3”, how can we correctly say “1 + 1 can equal 3”? What could that correctly mean? If you interpret it to mean the same as A1, it becomes trivial, and is clearly not what you want to say.
I think the problem is that you’re not paying enough attention to the context of these arithmetic symbols. Sometimes they are “in quotes”, i.e. words put into the mouth of some real or hypothetical speaker (as in A1). Other times they are words that you or I are using to make a statement on our own account (as in A2). In the first case we can hypothesise that some other language is being spoken. In the second case the context requires us to take the words in their familiar English sense. Every time you see or use an arithmetic symbol in this discussion, you should ask yourself what language the context requires us to take it in.
In my view, linguistic confusion is the biggest problem in philosophy. I agree with Wittgenstein that philosophy properly done is a battle against the bewitchment of our intellect by our language. It’s very hard to talk people out of a linguistic confusion, because the same confusion makes it hard for them to understand any explanation of the problem. That’s probably why you think you’re agreeing with me when you’re not, and why you find what I’m saying baffling. I don’t find your position baffling (though I find many individual sentences confusing), because I’ve been there myself.
Sorry for my lecturing tone.
P.S. Just after posting my last comment I realised you might object to my attributing to you the idea that 1 + 1 can equal 3, saying that’s too simplistic an interpretation of your position. So let me put it in terms of the sentence I quoted from you:
There are readings of this sentence which I could assent to. For example, if you meant that anyone speaking our language can correctly say “1 + 1 = 2, necessarily so”, then I’d agree with that. But since you seem unwilling yourself to say “1 + 1 = 2, necessarily so”, I take it this is not what you mean.
My point is not that the sentence is wrong on all possible readings, but that it’s ambiguous, and the fact that you feel it’s significant, together with the context of your arguments, imply that you mean it in a way I don’t agree with. The conditional implies that there can be other circumstances in which 1 + 1 does not equal 2. Otherwise, why say it? If all that’s being implied is A1, then I’d agree with you, but such a triviality doesn’t get you anywhere. And, if that’s all you meant, it would be better to say it explicitly.
Hi Richard,
You are right, in that the intended language and thus the meaning should be apparent to the reader, though too much pedantry can make for dull writing.
Let me ask you a question. Suppose you take a group of English-speaking physicists and mathematicians off in a space ship to observe a distant and weird planet where the laws of physics appear to be very different and strange things happen. Thus, someone puts an apple in an empty bowl, and then another one, and the observers look at the bowl and count three apples.
You ask these physicists and mathematicians to write a report on what they see, and to report back home on the physical, mathematical and logical system by which this world appears to operate. Thus they are writing a report in English for folks back home, trying to explain how alt-maths differs from the maths/logic back on Earth.
What sort of language and symbols are you going to allow them to use to convey this information? Now they could produce a report on alt-maths consisting solely of a set of entirely new symbols. But that’s not going to mean anything to the folks back home. So they’d need to provide some sort of mapping or translation between alt-maths symbols and the English/our-maths of our world. How would you suggest they do that?
Hi Coel,
I think it makes no sense to speak of a world operating by a mathematical or logical system. Mathematical systems are systems of thought that are useful for modelling the world. The pronouncements of scientists are their best attempts to model the way the world works. And they often find it useful to express their pronouncements in the precise language of mathematics. It may be that some new mathematical system (or addition to our mathematical system) would be more useful for modelling certain things in your hypothetical world. But we don’t need to go to another world to find such cases. New mathematics has often been useful to real scientists. (Whether that new mathematics was devised before or after its first use in science doesn’t matter as far as I can see.)
They can use any language they like, as long as they don’t conflate any new language with our pre-existing language. But I don’t think they even need any new language. You yourself managed to describe the other world without using any new language. True, you were very vague about how general the phenomenon is. Does it only apply to apples and bowls? If not, what sorts of things does it apply to, and what about the fact that sometimes it’s not clear what constitutes a single object? (What about half an apple, 3/4 of an apple, an apple with a hole in it, two halves of an apple connected by a trail of juice?) As the apple approaches and enters the bowl, at what point does the phenomenon kick in? Etc. I don’t see why you would necessarily need any new mathematical language/system to answer these questions, though I guess you might, depending on the answers.
I said earlier that one could perhaps invent a new arithmetic operator (“$”) suggested by the phenomenon you’ve described. (I used the words “modelled on”, which was probably a poor choice of words.) Even if that’s so, I don’t think your scientists need such an operator in order to describe the phenomenon.
There is no alt-maths for them to report on, unless they invent it. And in that case they would proceed in the way that mathematicians usually do. That would probably include giving definitions and/or axioms. As I argued in my very first comment, the basis of arithmetic was first established by informal practices. But mathematicians can also establish systems in more formal ways.
In short, we can invent new mathematical systems. It makes no difference whether we do it because those systems are useful for modelling our world, another world, or no world at all. Mathematical systems/languages are not dependent on the outside world.
Going back to something you wrote earlier:
I think this was a return to a concept that you earlier called “&”, and I’m going to call it that, not “+”, since I say it’s not equivalent to ordinary “+”, and it’s difficult to discuss whether they are equivalent if we use the same symbol for both. (I distinguish between “$” and “&”, because I’m taking “$” as referring to an arithmetic operator, though one as yet undefined apart from our knowing that 1 $ 1 = 3; whereas I don’t consider “&” even to be an arithmetic operator.)
In fact when you introduced “&” earlier, I asked whether you would accept that “&” was not equivalent to ordinary “+”, and you didn’t reply. (I guess I should have asked in a more neutral way, instead of trying to lead you into saying they’re not equivalent.) If they’re not equivalent, then you’re conflating different languages.
As far as I can see, what you’ve given is nothing like the way that mathematicians establish a new mathematical system or concept. In any case, I find it hard to make sense of it. It’s not clear what kind of mapping you have in mind. And do your symbols only map to activities with apples and bowls, or are these just representative examples? Nevertheless, it seems pretty clear to me that you want the following to be true in your proposed language: “1 & 1 = 2 in our world, and 1 & 1 = 3 in the other world”. But in ordinary language it’s not true to say “1 + 1 = 2 in our world, and 1 + 1 = 3 in the other world”. And I think you’ve accepted that. So “&” is not equivalent to ordinary “+”.
P.S. I wrote:
Oops. Silly me. Of course it couldn’t be used before it was devised. What I meant was something like this: Whether that new mathematics was devised specifically for a scientific use, or was devised without any scientific use in mind, but was then employed in science later…
Hi Richard,
They are not equivalent, no, because they are established in different ways and refer to different logical systems. However, if you were wanting to discuss similarities and differences between different logic systems then you would make informal comparisons between these.
They were supposed to be representative examples, and in that sense merely pointers to the possibility of a radically different logical system. The suggestion is that you start with a relatively informal observation of how things work, and gradually move to a more and more codified logical system that models the world one is looking at.
Hi Coel,
My definition- “Empiricism”: the belief that ALL knowledge is obtained ONLY via sensory experience, from the hardest facts to the wildest fantasies.
Blog quote: “..what basis do we have for supposing that our human intuition produces accurate knowledge about the universe? The first reason is that our intuition has been developed and honed over our lives based on our sense data about the world around us. Thus our intuition is very much an empirical product.”
Whilst of course agreeing with you that intuition IS empirical I think “Intuition” should properly refer only to our basic biological machinery which has little/no knowledge about “the universe”.
I ask “Suppose a baby was born devoid of all five senses what could its brain know about any external phenomena?”
Such a body/brain would be comatose. To survive at all, it must be using its extensive inborn, but read-only, knowledge: inherited unconscious knowledge, a huge vital Memory which controls/activates bodily functions, reflexes, instincts, Emotions and some Morality too. Evolved ‘reflex’ reasoning based on and passed down from countless ‘experiences’ of a myriad ‘successful’ ancestors. Empirical knowledge but at ‘umpteenth-hand’. (Making Evolution a workable, but extremely slow ‘scientific’ process?)
What then of other seemingly non-empirical knowledge? Dragons, fairies, sci-fi, Nothing, Infinity, or supernatural/irrational ones for the otherwise inexplicable? (Incidentally, all such ideas can have rational uses.) I maintain all ‘imagination’, however bizarre, never escapes the boundaries of EXISTING empirical knowledge. E.g. ‘Nothing’ and ‘Infinity’ are the extremes of our (empirical) finite, linguistically obtainable and can represent useful ‘knowledge’ as tools: yet fantasies, unobservable, boundless, impossible to ‘actualise’.
Blog quote: “1+1=2. Do you accept that statement as true? …why?”
Take the two comparable statements:
(1) “More is greater than Less”; (2) “5>3”
Both work in practice ONLY because they convey ideas that we commonly accept those symbols to represent: statement (2) contains similar information to (1) only with increased accuracy.
Any “more” must ALWAYS be greater than “less” just as any “5” must be greater than “3”. If intuition or external ‘truth’ be claimed to exist for statement (2) then so it must for (1) too. All you really do is ‘philosophise’ that “more” means “more”, “less” means “less”,etc. If 0215436789 were our *commonly-agreed* number sequence then “5<3" and "2+2=1" become 'true'.
Numbers are simply one part of LANGUAGE. I.e. a system of commonly-accepted symbols which may be held within one brain to represent knowledge, then used to convey that knowledge (using different forms of those symbols that are compatible with Touch, Hearing or Sight) to make closely-matching symbolic knowledge within another brain.
These supreme abilities separate us from and make us more intelligent than ALL other life on Earth, markedly so in the external permanently recorded forms, each of us having possible access to all human experience. Today's Global News, Plato, ancient Egyptians, Mathematics……..
I am sympathetic to the idea that a good deal of mathematics (it’s axioms and rules of inference) is abstracted from experience (this explains why it is useful for describing it). However, mathematics can also be regarded as free-floating- independent of experience, insofar as mathematicians are free to make up any axioms they please (like the game of chess). Thus, I think it is helpful to remember that there are really two kinds of mathematics: pure, formal or “game” mathematics, and empirical or “applied” mathematics, with cross-fertilization between the two endeavors. Game mathematics explains the sense of ‘certainty’ that mathematicians experience when they prove theorems, whereas empirical mathematics explains the applicability of mathematics to describing nature. For a chapter length exposition on this view see Simon Altmann’s book, Is Nature Supernatural? (Prometheus books).
As for logic being empirical, I am less convinced. To change our logic in light of experience we would have to presuppose a particular logical system according to which we could decide whether the logic in question is or is not empirically adequate. This leads either to regress or to circularity..
To qualify what was said above, logic may very well be empirically derived (either through learning or evolution), but it is less clear to me whether it can be revised in light of experience. Furthermore, (notwithstanding the views of paraconsistent and dialethic logicians) perhaps the law of non-contradiction, for example, holds in all possible worlds and is therefore indefeasible.
Pingback: The unity of maths and physics revisited | coelsblog
Pingback: Contra theologian Roger Trigg on the nature of science | coelsblog
Pingback: What is truth? – Thennicke
I saw this post and figured I’d add my 2 cents of information. I hope this contributes to ongoing discussion somehow.
Regarding (pure) intuition and mathematics in Kant it seems the issue in the Critique of Pure Reason is (in part) as follows:
Kant sees that judgments, such as ‘1 + 1 = 2’, are taken to be true even if we never employ the concepts of these terms in an experience (perhaps easier to use an example like ‘89,384 + 8,244 = 97,628’). He also sees that we can construct concepts in mathematics that do not need to be used in any experience in order for them to be valid (e.g., a chiliagon). This is where (pure) intuition comes in, however, not in a straight forward way. (Kant does think that if we couldn’t apply mathematical concepts to experience in some way then they wouldn’t have any validity for us, but more on that when discussing how math can apply to nature.)
For Kant, intuition is not a matter of thinking, but rather is the power corresponding to the receptive (or sensible) aspect of our experiences of objects. Constructing a square in our imagination isn’t like seeing a square, but the conditions of imagining a square are the same as experiencing a square. Kant argues that they both require the same form of representation: the pure form of intuition he calls space (as well as time). (Here space is a concept related to phenomenology and not so much physics.)
I this this could be fruitfully compared to empirical approaches to mathematics. For Kant, the experience of objects and shapes in nature will be an inspiration for the construction of mathematical concepts (all knowledge in Kant begins with experience, anyway). Whether this is accomplished by abstraction or something else I leave undecided, but Kant would at least insist that experience isn’t a strict limit what mathematical concepts we can construct.
As for how math applies back to nature/experience: time and space make all representation possible formally. Mathematical concepts are constructed on the basis of these forms, as well as experience/nature (so far as it is a representation for us). Because of this common source of cognition, mathematical concepts apply to nature as a matter of course (that is, if you happen to find a corresponding object in nature).
Of course, there are a lot of other details in Kant’s thought on this to compare, but I figured that these were the most salient for now.
Maybe this will be interesting, maybe not, but I figured I’d share.
Hi Erik,
Thanks for your contribution and thoughts on Kant:
But then we can ask why do we take them as true? I’d say that we do so because things like “89,384 + 8,244 = 97,628” follow tautologically from other more basic concepts, where those concepts are adopted because they model the empirical world and so are real-world verified.
We should bear in mind that what we call “intuition” is the product of our past encounters with the world, our own personal experiences and development growing up, and the long history of our ancestors’ interactions with the world now encoded into our genes via evolution.
Agreed, but mathematics is not unusual in that regard. One can do the same in areas of science. One can ask, given the “laws of physics” (= how the universe behaves), what range of possibilities are there? (Even when we have not directly observed those possibilities.)